对浙教版初中《数学》课本中一道例题的新探究

       我们的浙教版初中《数学》教材中，绝大多数例题和例题的教学方法是非常典型的，具有代表性，我们只要合理利用好这些例题，引导学生对这些例题进行探究，学习，就可以做到触类旁通的作用，使学生从题海中脱离，轻松学习，学生才可以从简单的模仿学习转变成研究型学习，真正做到思维训练。在教学中，笔者觉得教材对有些例题处理并不是很到位，下面就从笔者对教材中一道例题为例，和大家一起探讨课本例题的教学。

       
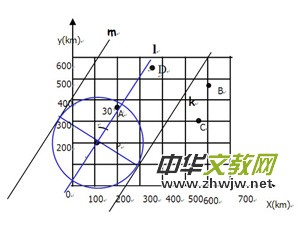
       浙教版九年级《数学》下册52页，“直线与圆的位置关系”第2课时”圆的切线的判定定理”中例题3，如图，如图，台风P(100，200)沿北偏东30°方向移动，受台风影响区域的半径为200km，那么下列城市A(200,380)，B(600，480)C(550，300),D(370，540)中，哪些受到这次台风的影响，哪些不受到台风的影响？
       本课的教学目标是掌握直线与圆相切的判定定理：经过半径外端，并且垂直这条半径的直线是圆的切线，以及会过圆上一点画圆的切线。本例教材是这样处理的，要解决城市是否受台风影响，关键是确定台风圈所扫过的区域。教材通过引导学生作出与台风圈⊙P运动路线l平行的两条切线m和k，则平行线m，k之间的区域为台风扫过的区域，通过观察判断点是否在这个区域中来判断城市是否受台风的影响。教材处理的重点是通过本例进一步巩固圆的切线的作法和判定定理，以及为下节课切线的性质打下铺垫。笔者在教学中，觉得教材这样处理还存在以下三个弊端：（1）教材对该题的画图是通过格点完成，降低了误差，如果没有格点，学生画图的准确性存在很大的问题。比如在区域的附近的点就很容易产生判断失误。（2）该题通过画图得出结论，缺乏理论依据，与数学学习的严谨性相悖，不利于学生理性思维的形成。  （3）例题只通过画图论证的方法得到结论，使教学还处于比较肤浅的状态，不能完全激发学生的求知欲望。笔者通过反复思索和组内集体备课的力量，最后是通过画图操作和理论论证结合的方法完成本例的教学的。
        笔者首先设置了三个问题，引导学生对本题进行如下探究：（1）台风圈⊙P运动过程中形成的区域为什么形状？如何作出这个区域？（2）这些城市是否受到台风影响，跟表示城市的点与区域关系如何？（3）如何用你学过的知识来论证你的结论？通过这三个问题的引导，学生首先作出与台风圈⊙P的运动区域，即平行线m，k之间的区域，然后得出在该区域的城市受台风影响，反之不在该区域的城市则不受台风影响的结论。对第3个问题的回答，只需要论证点到直线l的距离与半径之间的关系，即考虑点与圆的位置关系,就可以论证到结论。学生在教师的引导下，充分调动了思维的灵活性，通过交流讨论，得到了不同的解答方法，笔者归纳后，总结了如下三种常规方法求点到直线l的距离。
  （1）构造30°的直角三角形求直角边长。如图(1)：

      
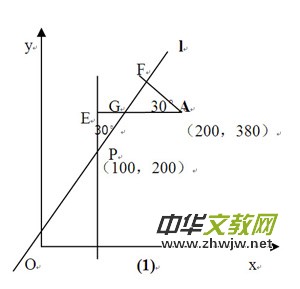
  过点P做PE⊥x轴,过点A作AE⊥PE，交直线l于点G。作AF⊥直线l，
  ∵∠GOE=30°，PE=180
  ∴EG==
  ∴AG=100-
  ∴AF==-90〈200
  ∴A在台风圈⊙P运动区域，受台风影响。
  同理可得：点B到直线l的距离为-140〉200。∴B不在台风圈⊙P运动区域，不受台风影响。
  点C到直线l的距离为-50〉200∴C不在台风圈⊙P运动区域，不受台风影响。
  点D到直线l的距离为-170〈200∴D在台风圈⊙P运动区域，受台风影响。
  (2)利用函数解析式和30°的直角三角形，求直角边长。如图(2)

    
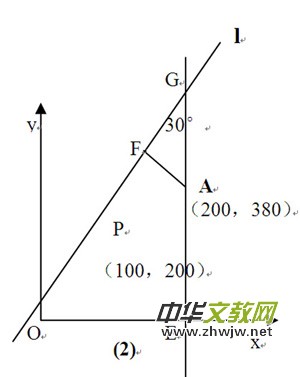
  由题可得直线l函数解析式为y=x+200-100
  过点A作AF⊥OP，AE⊥x轴，交直线l于点G。∴点G为(200，100+200)
  ∴GA=100+200-380=100-180,
  ∵∠FGA=30°
  ∴AF=AG=50-90,
  ∴A在台风圈⊙P运动区域，受台风影响。
  同理可得点B,C,D到直线l的距离.
  (3)构造直角三角形,利用等积法求高.如图(3)

    
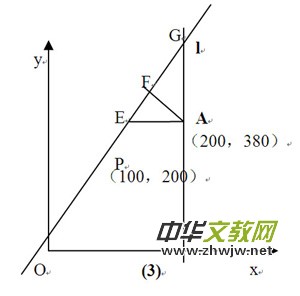
  作AG⊥x轴交直线l于点G，AE∥x轴交直线l于点E
  由直线l函数解析式为y=x+200-100。
  得点D坐标为(200，100+200)
  点E坐标为(60+100，380)
  ∴AE=200-(60+100)=100-60
  AG=100+200-380=100-180
  由勾股定理可得GE=200-120
  由△AEG面积求高可得

AF= =50-90。

  同理可得点B，C，,D到直线l的距离。
  在本例中,还可以通过求直线AF的函数解析式，再与直线l的函数解析式联立起来求垂足F点坐标，然后通过两点间距离公式求得A点到直线l的距离AF的长，由于该方法在次比较麻烦，笔者在此就不作详述。
  本例的教学，从作图到推理，不仅重新巩固了圆的切线的判定，而且通过论证过程与前面所学知识连贯起来，从感性上升到理性认识，也为今后高中阶段继续学习点与直线的距离的函数解析法打好基础。课本这类的问题还很多，只要教师对这一资源灵活合理利用，就能使学生的数学学习更加有效。