
�Գ��������������Ҳ����ѧ�������Ŀ�꣬��������ѧ��ѧ��ѧ�����ߣ�����ѧ��ѧ�ĺ������ݣ�Ҳ������������ѧ�Ļ����������ĶԳ����Ǻ�����һ���������ʣ��Գƹ�ϵ�����㷺��������ѧ����֮�У��������öԳ��������ܸ���ݵ�ʹ����õ������������ͨ�����������ĶԳ��ԺͲ�ͬ����֮��ĶԳ��������������������뺯���Գ��йص����ʡ�
һ�����������ĶԳ���̽��
����1.���� y = f (x)��ͼ����ڵ�A (a ,b)�ԳƵij�Ҫ������
f (x) + f (2a��x) = 2b
֤��������Ҫ�ԣ����P(x ,y)��y = f (x)ͼ������һ�㣬�ߵ�P( x ,y)���ڵ�A (a ,b)�ĶԳƵ�P����2a��x��2b��y��Ҳ��y = f (x)ͼ���ϣ��� 2b��y = f (2a��x)
��y + f (2a��x)=2b��f (x) + f (2a��x) = 2b����Ҫ�Ե�֤��
������ԣ����P(x0,y0)��y = f (x)ͼ������һ�㣬��y0 = f (x0)
�� f (x) + f (2a��x) =2b��f (x0) + f (2a��x0) =2b����2b��y0 = f (2a��x0) ��
�ʵ�P����2a��x0��2b��y0��Ҳ��y = f (x) ͼ���ϣ�����P���P�����ڵ�A (a ,b)�Գƣ�����Ե�����
���ۣ����� y = f (x)��ͼ�����ԭ��O�ԳƵij�Ҫ������f (x) + f (��x) = 0
����2. ���� y = f (x)��ͼ�����ֱ��x = a�ԳƵij�Ҫ������
�� f (a +x) = f (a��x) ��f (x) = f (2a��x) ��֤���������ߣ�
���ۣ����� y = f (x)��ͼ�����y��ԳƵij�Ҫ������f (x) = f (��x)
����3. ��������y = f (x) ͼ��ͬʱ���ڵ�A (a ,c)�͵�B (b ,c)�����ĶԳƣ�a��b������y = f (x)�����ں�������2| a��b|����һ�����ڡ�
��������y = f (x) ͼ��ͬʱ����ֱ��x = a ��ֱ��x = b����Գ� ��a��b������y = f (x)�����ں�������2| a��b|����һ�����ڡ�
��������y = f (x)ͼ��ȹ��ڵ�A (a ,c) �����ĶԳ��ֹ���ֱ��x =b����Գƣ�a��b������y = f (x)�����ں�������4| a��b|����һ�����ڡ�
�٢ڵ�֤���������ߣ����¸����۵�֤����
�ߺ���y = f (x)ͼ��ȹ��ڵ�A (a ,c) �����ĶԳƣ�
��f (x) + f (2a��x) =2c����2b��x��x�ã�
f (2b��x) + f [2a��(2b��x) ] =2c��������������*��
�֡ߺ���y = f (x)ͼ��ֱ��x =b����Գƣ�
�� f (2b��x) = f (x)���루*����
f (x) = 2c��f [2(a��b) + x]����������**��
��2��a��b����x��x��
f [2 (a��b)+ x] = 2c��f [4(a��b) + x]���루**���ã�
f (x) = f [4(a��b) + x],��y = f (x)�����ں�������4| a��b|����һ�����ڡ�
������ͬ�����Գ��Ե�̽��
����4. ����y = f (x)��y = 2b��f (2a��x)��ͼ����ڵ�A (a ,b)�����ĶԳơ�
����5. �ٺ���y = f (x)��y = f (2a��x)��ͼ�����ֱ��x = a����Գơ�
�ں���y = f (x)��a��x = f (a��y)��ͼ�����ֱ��x +y = a����Գơ�
�ۺ���y = f (x)��x��a = f (y + a)��ͼ�����ֱ��x��y = a����Գơ�
����4�붨��5�еĢ٢�֤���������ߣ���֤����5�еĢ�
���P(x0 ,y0)��y = f (x)ͼ������һ�㣬��y0 = f (x0)���ǵ�P( x ,y)����ֱ��x��y = a����ԳƵ�ΪP����x1�� y1������x1= a + y0, y1= x0��a ����x0= a + y1, y0= x1��a ����y0 = f (x0) ֮�е�x1��a = f (a + y1) ���P����x1�� y1���ں���x��a = f (y + a)��ͼ���ϡ�
ͬ����֤������x��a = f (y + a)��ͼ������һ�����ֱ��x��y = a����ԳƵ�Ҳ�ں���y = f (x)��ͼ���ϡ��ʶ���5�еĢ۳�����
���ۣ�����y = f (x)��ͼ����x = f (y)��ͼ�����ֱ��x = y ����Գơ�
���� ���Ǻ���ͼ��ĶԳ����б�
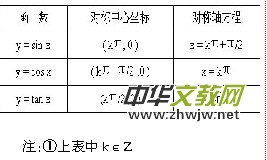
��y = tan x�����жԳ���������Ӧ����(k��/2 ,0 )�����״������Ϊ�ǣ�k��, 0��
�ġ������Գ���Ӧ�þ���
��1��������R�ϵķdz����������㣺f (10+x)Ϊż��������f (5��x) = f (5+x),��f (x)һ���ǣ� ��
(A)��ż������Ҳ�����ں��� (B)��ż���������������ں��� (C)���溯����Ҳ�����ں��� (D)���溯�������������ں���
�⣺��f (10+x)Ϊż��������f (10+x) = f (10��x).
��f (x)�������Գ��� x = 5��x =10 �����f (x)����10Ϊ��һ�����ڵ����ں�����
��x =0��y��Ҳ��f (x)�ĶԳ��ᣬ���f (x)����һ��ż��������ѡ(A)
��2���趨����ΪR�ĺ���y = f (x)��y = g(x)���з�����������f(x��1)��g-1(x��2)������ͼ�����ֱ��y = x�Գƣ���g(5) = 1999����ôf(4)=�� ����
��A�� 1999�� ��B��2000�� ��C��2001����D��2002�� ��
�⣺��y = f(x��1)��y = g-1(x��2)������ͼ�����ֱ��y = x�Գƣ�
��y = g-1(x��2) ��������y = f(x��1)����y = g-1(x��2)�ķ�������:y = 2 + g(x), ��f(x��1) = 2 + g(x), ����f(5��1) = 2 + g(5)=2001
��f(4) = 2001,Ӧѡ��C��
��3.��f(x)�Ƕ�����R�ϵ�ż��������f(1+x)= f(1��x),����1��x��0ʱ��
f (x) = ��x����f (8.6 ) = _________
�⣺��f(x)�Ƕ�����R�ϵ�ż������x = 0��y = f(x)�Գ��
�֡�f(1+x)= f(1��x) ��x = 1Ҳ��y = f (x) �Գ��ᡣ��y = f(x)����2Ϊ���ڵ����ں�������f (8.6 ) = f (8+0.6 ) = f (0.6 ) = f (��0.6 ) = 0.3
��4. ��f(x)�Ƕ�����R�ϵ��溯������f(x+2)= ��f(x),��0��x��1ʱ��
f (x) = x����f (7.5 ) = �� ��
(A) 0.5 (B) ��0.5 (C) 1.5 (D) ��1.5
�⣺��y = f (x)�Ƕ�����R�ϵ��溯������㣨0��0������Գ����ģ�
�֡�f (x+2 )= ��f (x) = f (��x)����f (1+ x) = f (1��x)�� ��ֱ��x = 1��y = f (x) �Գ��ᣬ��y = f (x)������Ϊ2�����ں�����
��f (7.5 ) = f (8��0.5 ) = f (��0.5 ) = ��f (0.5 ) =��0.5 ��ѡ(B)
�� ���ߵ�λ������ʡ�����صڶ�������
��һƪ��̸̸Сѧ��ѧ��ѧ�еı���


