激发兴趣多探究 灵活运用促效果

       如何提高数学教学质量，是每一个教师必须重视的问题。许多专家、名师都已作了深刻的探索。笔者根据多年的教学实践体会到“激趣·探究·活用”是提高教学效果较好的途径。下面就此问题，谈几点粗浅认识。
        一、激发兴趣，唤起学生的求知欲望
       平日里总有教师抱怨学生不认真学数学。其实，作为数学教师应该从自身查找原因。许多教师上课总是唱独角戏，一味地自己讲，学生听，课堂气氛沉闷，学生总处于被动接受知识的状态。这怎么能叫学生对你的课感兴趣呢？著名心理学家布鲁纳说过“学习最好的刺激是对所学教材的兴趣”。的确，兴趣将直接影响学习效果。林格伦曾对兴趣作过调查。结果表明，兴趣占影响学习成功因素的25%。所以，教师要想尽办法，上好每一节课，使单调乏味的学习变得活泼主动、妙趣横生。新的数学教材内容贴近学生的生活，教师应根据教材内容，巧设教学情境。充分挖掘其趣味性，抓住其与生活的联系点，引发学生兴趣，唤起学生的求知欲望，这样会收到事半功倍的教学效果。

        
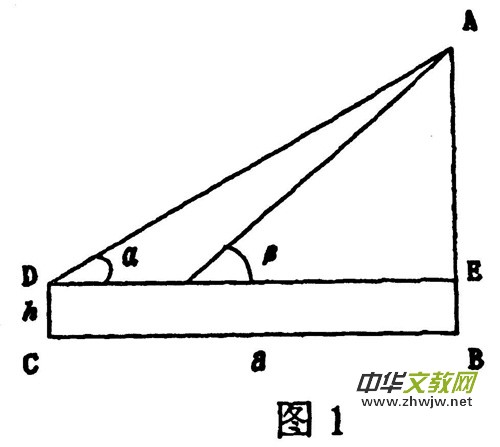
       在教学的具体实践中，教师可以运用实践法，引起学生对学习问题的关注。例如讲三角形内角和为180°时，让学生将三角形的三个内角剪下拼在一起，从实践中总结出三解形内角和为180°，这样来激发学生的学习兴趣。也可以联系生活实际，创设问题情景，刺激学生找寻答案的强烈欲望。如锐角三角函数的综合运用，具有一定的难度，为了激发学生的学习兴趣，教师可以根据学校周围的实物，如：自来水塔、或工厂烟囱、或其它建筑物，用学生已学过的知识，让学生用测角仪和卷尺等工具去测量某一建筑的顶端到水平面的距离（如图1所示）。这样，巧妙地把生活中的问题与所要学的知识联系起来，这样就能有效地激发学生学习的欲望。此外，还可以用观察法、演示法等等，去激发学生主动参与的意识。
       须注意的是：无论用哪种方法激趣，都要围绕本节课的教学内容去安排，不能喧宾夺主；其次，应让学生运用原有的知识和经验来含接新的知识，达到巩固和提高的目的。

    二、坚持探究，拓展学生的思维空间
       新课程标准强调学生是学习的主体，探究学习是课堂教学的核心。数学是思维的体操，数学教学的重点之一就是要培养学生的思维能力。引导学生探究是培养学生的思维能力的重要手段。因此在课堂教学中，教师要充分发挥学生的主体作用。创设良好的学习情境，启发学生积极探究，主动地获取知识，拓展其思维空间。
       采用分析判断、比较归纳、整体思考、变换角度、猜想推理等方法进行大胆的探究，都能有效地培养学生的思维能力。在具体实践中，教师应引导学生抓住问题的数字、图形、已知与未知，进行观察、分析、比较，寻找隐蔽条件，揭示新的“已知”，从而训练思维能力。例如：已知a、b、c为实数，且a2+b2+c2-2（a+b+c）+3=0，则a+b+c=____。可指导学生对此题整体思考进行探究，发现可用配方法整体处理，利用非负数的性质达到解题的目的。又如学习“菱形的性质”（如图2）时，可引导学生在复习平行四边形的性质、等腰三角形的性质、直角三角形的性质以及证明的基础上，进行实验操作、合作讨论探究出来，有学生会用“折叠法”的操作探究出：
       1.“菱形的四条边相等”、“菱形的两条对角线互相垂直”、“菱形的轴对称图形”。
       2.“菱形的每条对角线把菱形分解成两个等腰三角形”、“菱形的两条对角线把菱形分解成四个全等的直角三角形。”
       3.“菱形的对角线互相垂直”、“菱形的每一条对角线平分一组对角。”
       有学生会利用“面积之和法”得出并证明：“菱形的面积：S=■AC×BD。这样，学生既学到探究本领，又拓展了思维空间也增强了创新意识。这样的学习过程也符合构建主义“学习不是被动地接受信息刺激，而是主动地构建意义”这一理论。
       须提醒的是：教师组织学生质疑探究，既要开放，让学生各抒己见，又要有度，不能信马由缰，不能在“自主”旗帜下任意“放羊”。教师还要在学生在探索遇到困难时，作式子的变形、图形的变换、辅助线的添加等方面的点拨，起到“引导”“解惑”的作用。只有这样，才能真正达到探究是为了拓展学生的思维空间的目的。
    三、灵活运用，培养学生的迁移能力
       学生学习知识的终极目的是运用知识。如果只学不用，便成了知识的袋子。数学教学中，要教会学生如何灵活地运用所学知识。这里的运用有两方面的含义：一是运用学过的知识解决题目，二是运用数学知识解决生活中的问题。无论哪一种运用，都离不开总结规律，触类旁通。因此，教师要帮助学生总结规律，指导学生灵活运用知识，从而培养学生的迁移能力，达到叶圣陶先生提出的“教是为了不教”的目的。例如，在图3中，大小⊙O同心，大圆半径为R，小圆半径为r，AB为大圆的直径，P为小圆上任意一点。求证：PA2-PB2为定一长。

       可引导学生根据这些规律来学习：1、线段的平方应履与“勾股定理”有关联。2、因为P为小圆上任意一点，把P点位置特殊化（如图4），作出恰当的辅助线，找出大圆半径、小圆半径和PA、PB的长度四者之间的等量关系。3、根据“垂径定理”可得到PA与PB的等量关系，求出了PA2+PB2的定长为2（R2+r2）。
       数学中利用规律来解决的问题很多，像判别一元二次方程的根，就要引导学生根据根与系数的关系来解决；数形结合可解决有关方面和函数的问题或解决与函数有关的代数、几何综合性问题等。以灵活的教法，促进教学效果的提高。
       教师还要扣紧现实生活与课本知识的联系，引导学生总结规律，灵活地运用于解决生活问题之中。如教学正多边形及其性质以后，可以以学校周围相类似的建筑为例，引导学生总结出正多边形的性质的共同点，设计出为外墙密贴瓷块或地板密铺地砖的方案。这样，引导学生不断地总结规律并灵活的运用，不仅增添了学生的学习兴趣，也拓宽了学生的思维空间，更培养了学生的创新精神，运用知识的乐趣又促使他们投入到更深更广的探究之中，形成良性循环。
       综上所述，教师要因材施教，要以新课标的要求为指导，调动学生学习兴趣，巧设教学情境，多让学生质疑，灵活运用所学知识，达到提高教学水平。
                                                                      （作者单位：广东省五华县华东中学）