漫话数学课改中的“放、引、点、收”
广东省汕头市龙湖区外砂华侨中学 胡会英
教无定法。但教师应根据学生实际，教材内容进行教法改革。笔者从多年教学实践总结，认为对初中学生，按新课标要求，教学过程中，可采用“放、引、点、收”的方法。下面就此问题，谈谈几点不成熟的认识。
一、放开。
放：教法放灵：学法放活；知识面放宽、拓广。教师在教学中要敢于大胆放开，激发学生学习数学的兴趣，挖掘学生的潜能，发展学生的发散思维和主动获取与处理信息的能力。教师可以做如下的试验。
例一（学习课题）：等腰三角形的性质
预习问题：等腰三角形的性质有哪些？正三角形呢？你能证明吗？
顶习方式：阅读课文、实验操作、查阅资料、网上查询、交流讨论等。
学习方式：讨论、交流、演示。
综合课堂上学生的答案可概括为四个层次：
A、“等边对等角”、“等腰三角形的三线合一”、“等腰三角形的轴对称性”
B、等腰三角形两底角的平分线（腰上的高）相等。
C、等腰三角形底边上的点到两腰的距离的和等于腰上的高（证明如图1\2）。
D、等边三角形不但具有“三线合一”，而且还具有“五心相印”。
探究发现，让全班同学惊讶的是说出D层答案的学生，他的成绩一般，但他是个“网通”。课堂上他思路清晰地解了“五心”的概念、“相印”的含义。他的回答引起了全班同学的好奇。学生激情高涨，气氛活跃，意犹未尽，流连忘返。
二、巧引。
创设合适的问题情境，巧用生动、有趣的引入，能激发学生找寻答案的强烈欲望，引起学生对学习问题的高度关注，增强学生克服困难的勇气，使学生在学习活动中能主动、积极地参与。
例二（活动课题）：测量隔河相望的楼高（图3)
这课题是三角函数的综合运用，具有一定的难度，但实用性强。要让学生能顺利完成本课题的测量任务，教师必须提出一个能引起全体学生产生共鸣的话题，激发学生积极参与的兴趣。
教师可以发问：
1、世界上最高的山峰是 ，高度是 千米。
2、最近由哪国的测绘队测出新的数据？3、他们是如何测量的呢？你能行吗？
问题的提出，引起了学生的极大兴趣，异口同声地回答——珠穆朗玛峰，8844.43米……。问题3把学生引入思考的状态，使他们产生了极大的困惑，甚至对问题中的数据答案产生了质疑。这时，教师可以用一句煽动性的话语：“带上一个量角器和一把尺子，领你们测量高峰去！”可能学生一听，马上精神振奋，迫切地想得到测量的方法。
通过巧妙引入，学生对本课题产生了浓厚的兴趣，整个测量活动学生始终表现得主动、积极，合作、融洽，顺利完成了测量任务。各小组测量得出的数据非常接近，误差很小，使“小专家”们感到无比自豪和骄傲。
三、精点。
对于学生在探索或解题过程中遇到困难和出现问题时，教师的精辟点拨能使学生在比较中拔雾识“途”，明理悟“道”，起到“解惑”的作用。
1、教师可给学生的操作探究作点拨。
学生的操作探究是对所学知识的运用和创新。在学生的操作过程中，教师应启发学生运用所学的知识或构建数学模型作为操作的理论依据。
例三（操作课题）：用20cm的铁丝请同学们围成面积最大的矩形
学生在操作过程中，反复地实践、操作、猜测，个别学生很快猜测出了结果。
如图4，但无法论证，陷入了迷茫。教师可抓住时机，启发学生设立变量，构建数 图4
学模型，求出面积最大矩形的长、宽。教师的点拨，使学生的思维茅塞顿开，他们
顿时明白：原来这是正方一道二次函数极值的迁移问题。并很快找到论证的方法。
2、给学生的解题技巧作点拨
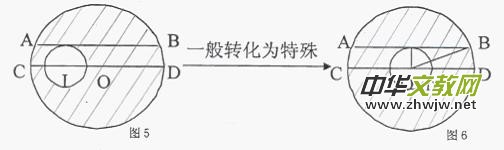
例四（解答问题）：在图5中，两个圆内含，小圆的圆心I在大圆0的直径CD 上，长为4厘米的弦AB与CD平行且与小圆相切，求图中阴影部分的面积。
学生分析：阴影部分的面积＝大圆的面积－小圆的面积，但无法一一求出大圆的半径和小圆的半径。
老师点拨：把小圆向右平移，使两圆构成同心圆，再作出恰当的辅助线，找出大圆半径、小圆半径和弦AB的长度三者之间的大小关系。
通过点拨，学生很快作出了恰当的辅助线，如图6，从而求出了阴影部分的面积。
此外，教学中，教师还应注意给学生的审题阅读和观察识图等作恰到好处的点拨。
四、妙收。
对所学知识，教师应该引导学生做系统、科学的复习。教师不仅要充当捕获知识的“撒网”高手，还应把学生培养成“收网”的能人。
1、小节复习是知识的积累过程，教师可要求学生坚持写学习笔记，记录小节知识的探究方法、过程、结论及应用，写出探究的感受，提出创新的设想。
2、章节复习是学生巩固知识的重要环节。教师应该引导学生选用恰当的方式，力求生动形象，条理清楚，能给学生留下深刻的印象，为学生提供有效的记忆方法。
例五（复习课题）二次函数。
二次函数复习时，教师可引导学生巧用数形结合如图7，由特殊的形式y=ax2通过“平移”、“旋转”，从而得出二次函数的种种类型，尽现二次函数中的丰富知识，让学生达到以数思形、以形释数的高度概括的奇妙效果。
3、总复习，引导学生分专题板块进行复习。把初中数学划分为三个板块：空间与图形、数与代数、概率与统计。启发学生构造板块网络图，进行全面系统的知识收网。
在教学中注重“放开、巧引、精点、妙收”，让学生在经历探索过程中体验到“做数学”的不易，并在互相合作、交流中享受到数学带来的快乐，从而达到了学生愿学、能学、会学的目的，大大提高了数学教学效果。
